Der erweiterte euklidische Algorithmus

Mit Hilfe des euklidischen Algorithmus kann man zu zwei Zahlen den größten gemeinsamen Teiler (ggT) effizient berechnen. Modifiziert man den Algorithmus ein wenig, kann man ihn dazu verwenden, zu einer Zahl 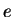$e$ das inverse Element 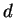$d$ in einer Modulo-Restgruppe zu finden. Das heisst, 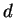$d$ ist die Zahl, welche mit 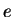$e$ multipliziert anschließend um 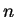$n$ reduziert 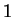$1$ ergibt. Mathematisch lässt sich das Problem wie folgt beschreiben:

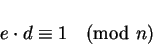$$e \cdot d \equiv 1 \pmod{n}$$ (2)

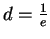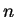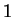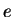Das inverse Element ist nicht einfach $d = \frac{1}{e}$, da wir es mit Modulo-Multiplikationen zu tun haben. Es gibt aber immer Zahlen, die, wenn sie um $n$ reduziert werden, $1$ ergeben. Eine solche Zahl, die zudem noch durch $e$ teilbar ist, ergibt bei der Division durch 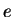$e$ das gesuchte inverse Element $d$.

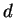Die genaue Anwendung und Funktionsweise des erweiterten euklidischen Algorithmus würden den Rahmen dieser Arbeit sprengen, deswegen sei an dieser Stelle auf [1], Seite 97 und [4] verwiesen, wo der erweiterte euklidische Algorithmus vorgestellt wird.