Obwohl das Verfahren an sich so einfach ist, wie in (15)
und (16) beschrieben, macht die Größe der
Zahlen durchaus Probleme. Selbst wenn man 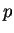 und
und 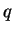 extrem klein wählt
(unter 100) ist
extrem klein wählt
(unter 100) ist 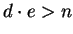 , da
, da
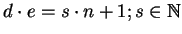 . Das heißt:
. Das heißt: 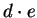 ist um eins grösser als ein
Vielfaches von
ist um eins grösser als ein
Vielfaches von 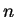 , also mindestens
, also mindestens 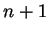 . Das Problem ist also, mit
einer hundertstelligen Zahl zu potenzieren - eine Aufgabe, die auch
für moderne Computer eine Herausforderung darstellt. Man verwendet daher
einen Trick, der unter anderem in [2] beschrieben wird:
. Das Problem ist also, mit
einer hundertstelligen Zahl zu potenzieren - eine Aufgabe, die auch
für moderne Computer eine Herausforderung darstellt. Man verwendet daher
einen Trick, der unter anderem in [2] beschrieben wird:
Um beispielsweise
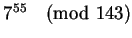 zu berechnen, stellt man den
Exponenten
zu berechnen, stellt man den
Exponenten 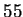 zunächst als Summe von Potenzen von 2 dar:
zunächst als Summe von Potenzen von 2 dar:
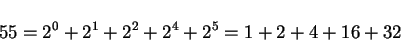 |
(17) |
Damit kann man die Potenz umformen zu:
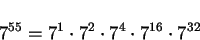 |
(18) |
Nun berechnet man zunächst die kleinen Faktoren mit Hilfe der
Modulo-Multiplikation:
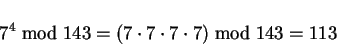 |
(19) |
Jetzt kann man die größeren Potenzen mit Hilfe der Ergebnisse bei den
kleineren Potenzen nach dem gleichen Schema berechnen:
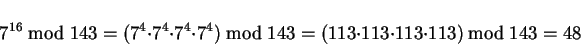 |
(20) |
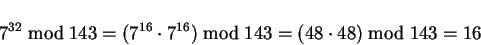 |
(21) |
Die Modulo-Multiplikation verhindert, dass die Zahlen zu groß werden und
reduziert zugleich noch die Anzahl der notwendigen Rechenschritte.
Florian octo Forster, 2003-01-31
![]() zu berechnen, stellt man den
Exponenten
zu berechnen, stellt man den
Exponenten ![]() zunächst als Summe von Potenzen von 2 dar:
zunächst als Summe von Potenzen von 2 dar: