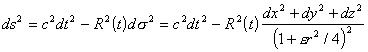Hans Ertel and Cosmology

By Wilfried Schroeder and Hans-Juergen Treder

Abstract: This paper deals with Hans Ertel's contribution to fundamental cosmological problems and with the irrelevance to geophysics. Ertel's studies are related to Einstein's relativistic physics, Eddington's large numbers in cosmology, and to other problems.

The main thesis of Hans Ertel's studies based on Einstein's, Eddington's, and Weyl's work can be expressed today with Einstein's final sentence concluding his efforts to establish a unified field theory of space, time, and matter. This reads as follows: “From the, quantum phenomena it appears to follow with contents that a finite system of finite energy can be completely described by a finite set of numbers (quantum numbers)” (Einstein 1955, p. 165).

The cosmological world models with a closed 3-dimensional (spherical) space (e = + 1 and with l > 0) state that the universe is a system like that. The problem implied was also called a possible "algebraification" of physics by Einstein (instead of its geometrization according to the program of the general theory of relativity).

The relativistic cosmology simplifies Einstein's gravitational equations and their application to very big systems - namely to the universe itself - by demanding a perfect "Copernicanism." According to this idea, there are no extended inhomogeneities "en gros" in the universe, and there never existed such ones. This makes it possible to interpret astronomical information coming from electromagnetic waves. Weyl and Robertson have shown that such a perfect Copernicanism leads to the fact that the cosmological space-time-world V_k conforms to Minkowski's space-time in the special theory of relativity. In this special case the same wave optics can be derived from the Maxwellian equations of the electromagnetic field as that in the special theory of relativity (Weyl's cosmological principle).

1. WORLD MODELS

  Furthermore, cosmology demands the existence of a universal synchrony in Einstein's sense: The world V₄ is then the imprimitive topological product of 3D space coordinates with time t:

V₄ = V₃ x ct                                                                           (1)

This means for a conformal plane V₄ that V₃ possesses again a constant curvature e = + 1, 0, - 1. This is the Robertson-Walker metric

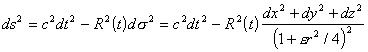                                     (2)

e = + 1 means a closed (spherically curved) 3D space V₃. For e = - 1 and e = 0 the cosmos is infinite in space.

Weyl's principle and the universal Einsteinian synchronism [ Eq. (2) ] define a homogeneous and isotropic cosmic matter according to Einstein's gravity equation that is a pure function of the cosmic time t. In this case Friedmann's equations are valid:

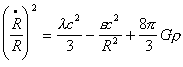                                                                                                (3)
and from it,

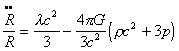                                                             (4)

Here r(t) means the mass density, rc² is then the energy density, and p(t) is the pressure. p and r are connected by the dynamic equation

                                                             (5)

which simplifies for pure, pressure-free matter (p = 0) to the conservation of mass, namely to

r₀R₀³  =  rR³  =  const

It follows from Eq. (4) that for l ≤ 0 the world radius R(t) has no minimum and R < 0 is always valid. However, if  l > 0, then there is a minimum world radius and the acceleration   of the expansion velocity of the cosmos may also be zero.

The correct model of such a cosmos is then a spherical, finite one, which was introduced into physics by Einstein in 1917. The mass of this cosmos is limited; it is M = 2p²rR³ = const.

Eddington supposed that the initial site of the cosmos was an unstable Einsteinian cosmos which had existed for an infinitely long time. At that time (i.e., at the time when t ® w), it was

and also

which means that R = l^-1/2. Therefore the mass of this cosmos is always equal to the Einsteinian mass when it collapses due to its instability:

M = M_Einstein = 0,5pc²G^-1l^-1/2

This Eddington-Lemaitre cosmos had its maximum density g₀ at the time t = - w, and at t ® w it transforms into the Sitter cosmos

R = l^-1/2 exp((l/3)^-1/2 ct)

of a vanishingly low mass density r ~ R^-3  ~ c^-3 (l/3)^-1/2 ct.

Eddington applied his numerical relations to this world model in which there never existed a singular state of infinitely high energy density, and therefore there was no "big bang." On the contrary, Ertel considered the general case of a "Friedmann-Lemaitre cosmos" with e = + 1 and of total mass

M > 0,5pc²G^-1l^-1/2

This cosmos started with an infinitely high density r ~ 1/R³  ~ 1/t² at the time t ® 0, i.e., with a big bang (when a radiation energy and p ~ 1/R⁴ could also exist but later they became small in compan'son with r ~ 1/R³ (see Ertel, 1935a-f, 1936, 1938a-c).

In this case, the cosmos reached a turning point R´´₀ = 0 at a time t = t₀ > 0 when r₀ = lc²/4p. This happened when in the case of a mass

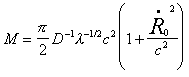
the radius of the world became

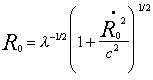
The duration of this state of minimum expansion velocity can be very long.

For the Hubble number is

H₀² = lc² - c²/ R₀²

The smaller the difference l - 1/ R₀² is, the longer the quasi-stationary state of a very slow expansion remains. The quantum physical eigenstates, which have existed in a primary Einsteinian cosmos for an infinitely long time according to Eddington's cosmological scenario (1933), came into being within a finite time in the quasi-stationary phase of the Friedmann- Lemaitre cosmos according to Ertel (1935). Thus, the cosmological numerical values are "frozen in quantum numbers" of this state of slow expansion with  and  which came into being after the big bang at t = 0.

Following this phase, which was called "atome primitive" by Lemaitre (later in 1948), the expansion accelerated again, and finally the Friedmann-Lemaitre cosmos goes asymptotically into a de Sitter cosmos at t ® +w.

Thus, Ertel's scenario applies the quantum-cosmological reasoning from the Eddingtoan-Lemaitre model with M = Mo = p/2G^-1l^-1/2c² to the Friedmann-Lemaitre cosmoses in which M > M₀, and considers a quasi-stationary state with H₀²  » (l - 1/R₀²) c²,   at time t ® w as the base for the cosmological numerical relations. Thus Ertel has unified Eddington's quantum cosmology with the idea of a primary "big bang."

2. THEORETICAL CONSEQUENCES AND STARTING POINTS

Einstein's complete general-relativistic field equa.tions contain three universal constants: the velocity of light c which transforms time t in the special theory of relativity (STR) into a fourth coordinate of Minkowski's space-time-world, x⁴ = ct Einstein's gravity constant K = (8p/c⁴) G, where G is the Cavendish-Newtonian constant in the Newtonian gravity law, and Einstein's cosmological constant l with the dimension of inverse surface being a measure of curvature in the space-time world. With these constants Einstein's equations are

R_ik – ½ g_ik R + lg_ik = kT_ik

where R_ik is the once contracted tensor (the Ricci tensor), R = R^l_l is the curvature scalar, and g_ik is the metric tensor of a Riemann 4D space-time world. The tensor at the right side holds together the remaining physics, the energy and stress distribution of matter particles and fields as a “matter-tensor” T_ik. The comparison of this matter and the existence of stable bodies and processes, being applicable as a scale in measurements of space and time, are ensured by the existence of Planck's effect quantum h.

With the help both of G and c, or both of h and c, a length can be attributed to each mass M. These are on the one hand the gravity radius GM/c² and on the other hand the Compton wavelength h/Mc. Planck discussed this problem earlier and considered h, c, and G as fundamental constants of physics. These hypothetical particles are called today Planckions of the mass M_p = (hc/G)^½  and are ideal test bodies of physics according to him. All other physical constants could be expressed in the programs of a relativistic gravity theory as multiples of Planck's quantities.

Planck has already noted that the elementare charge e is of the same physical dimension as (hc)^½. lt is valid that

e² = ahc

where a » 1/137 is Sommerfeld's fine structure constant applied in the quantum theory. As early as in 1908 Einstein demanded that the computation from h and e should be an aim of the quantum theory of electrons and of the Maxwellian field. The linear Maxwellian equations are, however, unable to determine the elementary charge e.

For gravity the large number w = hc/Gm² = 10³⁹ is the inverse Sommerfeld number. Using Eddington's "big cosmic number" N,

N = c³/Ghl » w³ = 10¹¹⁷

is valid for M:

M » c²G^-1l^-½  = N^½ M_p = N^2/3 m

where m is the mass of a proton (generally the mass of a stable baryon). In this case, the "total effect of the cosmos" is defined as

Mcl^-½  = c³G^-1l^-1 : Nhc (the Haas relation)

Thus, the mass m of the stable elementary particles is determined by the cosmos (this corresponds to the Einsteinian Interpretation of Mach's principle). m=h^2/3G^-1/3l^1/6; thus for l ® 0 the rest of the mass of the elementary particles would disappear. After Weyl the Haas relation can be written as

GM² = G^-1c⁴l^-1=Nh

This is the cosmological counterpart of Planck's relation:

GM²_p = hc

Eddington supposed that these algebraic numerical relations belong to the unstable, stationary Einsteinian cosmos. Eddington's, Weyl's, and Haas' numerical relations should be eigenvalues of a general-relativistic quantum theory in the closed stationary Einsteinian space, which have existed and will exist for an "infinitely longtime" as presumed in the Eddington-Haas model. In this case, these states are "frozen-in quantum states."

Ertel has shown that these special models for the Eddington, Weyl, and Haas relations between macro- and microcosmos are not necessary. It is possible to deduce the same relations from the General Friedmann- Lemaitre model up to a factor of the order of magnitude of one (e = 1, l > 0). Thus, they are frozen-in quantum states from the phase of the cosmos when the expansion of the world was very slow:

H² = lc² – c²/R₀²,        with R₀² = l^-1(1+ R´₀²/c²)

This state was also quasi-stationary. Before it, the world came into being through a big bang and after the stationary state the world is asymptotically transforming into a de Sitter cosmos with

H² = lc^2/3

in Eddington's model. According to Ertel the Eddington-Haas relations are principally not coupled with the primary Einsteinian cosmos and assume a big bang, too.