Nächste Seite: Das RSA-Verfahren Aufwärts: Das Merkle-Hellman-Verfahren Vorherige Seite: Generierung des private key Inhalt Index
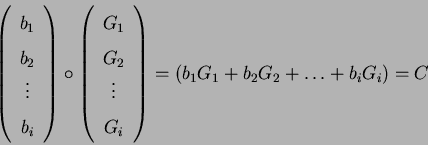 |
(8) |
Um ,,den Rucksack wieder auszupacken`` benötigt der Empfänger lediglich
![]() und
und ![]() . Mit folgender Rechnung erhält er eine Summe
. Mit folgender Rechnung erhält er eine Summe ![]() , die sich
aus Elementen der Menge
, die sich
aus Elementen der Menge
![]() zusammensetzt. Da in dieser Menge
jedes nächst größere Element größer ist als die Summe aller
vorherigen Elemente, kann leicht auf die einzelnen Elemente geschlossen
werden.
zusammensetzt. Da in dieser Menge
jedes nächst größere Element größer ist als die Summe aller
vorherigen Elemente, kann leicht auf die einzelnen Elemente geschlossen
werden.
| (9) |
Florian octo Forster, 2003-01-31